迈向核外 ND-数组

这项工作得到了 Continuum Analytics 和 XDATA 项目的支持，作为 Blaze 项目的一部分

要点速览： 我们提出了一个以任务为中心的计算系统，展示了一个使用核外 nd-数组的示例，并征求意见。

注意：本文不以用户为中心。它适用于库开发者。

动机

最近的 Notebook（链接 1、2）描述了 Blaze 如何通过以下阶段处理核外单数据集表格计算。

将数据集分割成块
对每个块应用一些计算
合并结果（希望更小）
将另一项计算应用于合并后的结果

步骤 2 和 4 需要对**做什么**工作进行符号分析；Blaze 在这方面做得很好。步骤 1 和 3 更多地是协调数据**去哪里**以及计算**何时**执行。

这种设置对于广泛的单数据集表格计算是有效的。但对于更复杂的场景则无效。Blaze 目前还没有一个好的目标来描述复杂的块间数据依赖。分解数据和安排计算的模型（1 和 3）过于简单。

一个复杂场景的好例子是 nd-数组矩阵乘法 / 点积 / 张量收缩。在这种情况下，分块方法具有更复杂的通信模式。本文旨在寻找一个简单的框架，使我们能够表达这些模式。它旨在寻找上面步骤 1 和 3 的替代方案。

任务调度

解决此问题的常用方法是将计算描述为二分有向无环图，其中节点是计算和数据，边表示计算将哪些数据片段作为输入并输出哪些数据片段。

对于这个问题，存在许多解决方案，包括理论算法和已实现的软件。请原谅我再次描述另一个系统。

`dask`

我们使用一种低技术含量的任务依赖图表示。我们使用键值对字典，其中键可以是任何可哈希标识符，值是以下之一：

一个值，例如 1
一个包含函数和参数的元组，例如 (inc, 1)。这类似于 s-表达式，应解释为未求值的 inc(1)
一个包含函数和参数的元组。参数可以包含其他键，例如 (inc, 'my_key')

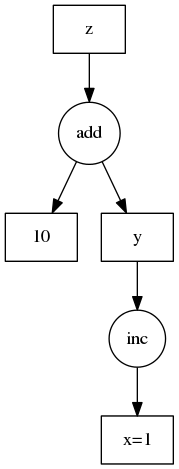
通过示例可以更清楚。我们在右侧展示了这个示例。

d = {'x': 1,
     'y': (inc, 'x'),
     'z': (add, 'y', 10)}

dask 库包含一个小的参考实现，用于获取此任务图中与键关联的值。

>>> import dask
>>> dask.get(d, 'x')
1
>>> dask.get(d, 'y')  # Triggers computation
2
>>> dask.get(d, 'z')  # Triggers computation
12

原则上，这可以由各种不同的实现来执行，每个实现都有针对分布式计算、缓存等的不同解决方案。

Dask 还包含用于构建此图的便利函数。

>>> dask.set(d, 'a', add, args=['x', 'y'])

尽管这主要是为了帮助那些不习惯将括号放在函数调用左侧从而避免立即执行的人

>>> # d['a'] =  add( 'x', 'y')  # intend this
>>>   d['a'] = (add, 'x', 'y')  # but write this to avoid immediate execution

为什么是低技术含量？

这些“图”只是元组的字典。值得注意的是，我们在构建图之后才导入 dask。框架投入非常轻。

问：为什么我们不构建 Task 和 Data 类并构建一个 Python 框架来正式表示这些东西？
答：因为人们必须学习并接受那个框架，而且这很难推广。字典更容易推广。它们也容易翻译成其他系统。此外，我可以在几十行代码中编写一个参考实现。

很容易构建函数来为各种应用创建这样的 dict。如果您已经读到这里，很可能您已经理解了规范。

ND-数组

我想将核外 ND-数组算法编码为数据。我编写了一些函数来创建 dask 风格的字典，以帮助我描述一类不错的块状 nd-数组计算。

以下部分是将这些想法应用于数组计算领域的具体示例。这只是一个应用，不是任务调度核心思想的一部分。任务调度和 dask 实现的核心思想已在上面介绍过。

从数组中获取块

首先，我们将一个大的、可能是核外的数组分解成块。为方便起见，在这些示例中，我们使用内存中的 numpy 数组而不是磁盘上的数组。如果您想查看在磁盘数据上进行实际的核外点积，请跳转到最后。

我们创建一个函数 ndget 来提取单个块

>>> x = np.arange(24).reshape((4, 6))
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23]])

>>> # Cutting into (2, 3) shaped blocks, get the (0, 0)th block
>>> ndget(x, (2, 3), 0, 0)
array([[0, 1, 2],
       [6, 7, 8]])

>>> # Cutting into (2, 3) shaped blocks, get the (1, 0)th block
>>> ndget(x, (2, 3), 1, 0)
array([[12, 13, 14],
       [18, 19, 20]])

现在我们创建一个函数 getem，它创建一个 dict，该字典使用 ndget 函数来提取所有块。这在我们的字典中创建了更多的 key，每个块一个。我们通过数组的键后跟块索引来命名每个键。

getem：给定一个大的、可能是核外的数组和块大小，将该数组分解成许多小块

>>> d = {'X': x}  # map the key 'X' to the data x

>>> getem('X', blocksize=(2, 3), shape=(4, 6))
{('X', 0, 0): (ndget, 'X', (2, 3), 0, 0),
 ('X', 1, 0): (ndget, 'X', (2, 3), 1, 0),
 ('X', 1, 1): (ndget, 'X', (2, 3), 1, 1),
 ('X', 0, 1): (ndget, 'X', (2, 3), 0, 1)}

>>> d.update(_)  # dump in getem dict

因此我们有一个原始数组 x，并使用 getem，我们描述了如何使用函数 ndget 为每个块从 x 中获取多个块。

ndget 实际上对数据进行操作
getem 创建一个 dask dict，描述 ndget 应该对什么进行操作

我们还没有真正工作。只有当我们最终在某个块的相应键上调用 dask.get 时，我们才真正工作。

>>> dask.get(d, ('X', 1, 0))  # Get block corresponding to key ('X' ,1, 0)
array([[12, 13, 14],
       [18, 19, 20]])

为方便起见，我们使用 numpy.ndarrays。这也适用于任何支持 numpy 风格索引的对象，包括 h5py.Dataset、tables.Array 或 bcolz.carray 等核外结构。

示例：极易并行计算

如果我们有一个简单的函数

def inc(x):
    return x + 1

我们希望将此函数应用于数据集的所有块，原则上我们可以将以下内容添加到我们的字典中。

>>> d.update({('X-plus-1', i, j): (inc, ('X', i, j)) for i in range(2)
                                                     for j in range(2)})
>>> dask.get(d, ('X-plus-1', 0, 0))
array([[1, 2, 3],
       [7, 8, 9]])

我们使用诸如 ('name', i, j) 之类的键来引用数组的第 i,j 个块，这只是一个附带的约定，并非 dask 本身固有的。将元组用作键不应与在值中使用元组来编码未求值函数混淆。

索引表达式

广泛的数组计算都可以用索引表达式来编写

\(Z*{ij} = X*{ji} \;\;\) – 矩阵转置

\(Z*{ik} = \sum_j X*{ij} Y\_{jk} \;\;\) – 矩阵乘法

幸运的是，这些算法的分块版本看起来基本相同。为了利用这种结构，我们创建了函数 top 用于**张量操作**（欢迎提出更好的命名建议）。这可以编写如下所示的分块转置索引操作

>>> top(np.transpose, 'Z', 'ji', 'X', 'ij', numblocks={'X': (2, 2)})
{('Z', 0, 0): (numpy.transpose, ('X', 0, 0)),
 ('Z', 0, 1): (numpy.transpose, ('X', 1, 0)),
 ('Z', 1, 0): (numpy.transpose, ('X', 0, 1)),
 ('Z', 1, 1): (numpy.transpose, ('X', 1, 1))}

第一个参数 np.transpose 是应用于每个块的函数。第二个和第三个参数是输出的名称和索引模式。接下来的参数是输入的键和索引模式。在这种情况下，索引模式是反向的。我们在调用函数 np.transpose 后，将第 ij 个块映射到输出的第 ji 个块。最后，我们有 numblocks 关键字参数，它给出了输入的块结构。索引结构可以是任何可迭代对象。

矩阵乘法

我们用输入中重复但输出中没有的索引来表示张量收缩（如矩阵乘法），如下所示。在下面的示例中，索引 'j' 是一个收缩的哑索引。

>>> top(..., Z, 'ik', X, 'ij', Y, 'jk', numblocks=...)

在这种情况下，函数接收一个数据块的迭代器，该迭代器遍历哑索引 j。我们创建一个这样的函数，它接收方形数组块的迭代器，对每对块进行点积，然后将结果求和。这是传统分块矩阵乘法算法的最内层循环。

def dotmany(A, B):
    return sum(map(np.dot, A, B))

通过将此逐块函数与 top 结合，我们得到了一个核外点积。

>>> top(dotmany, 'Z', 'ik', 'X', 'ij', 'Y', 'jk',  numblocks={'X': (2, 2),
                                                              'Y': (2, 2)})
{('Z', 0, 0): (dotmany, [('X', 0, 0), ('X', 0, 1)],
                        [('Y', 0, 0), ('Y', 1, 0)]),
 ('Z', 0, 1): (dotmany, [('X', 0, 0), ('X', 0, 1)],
                        [('Y', 0, 1), ('Y', 1, 1)]),
 ('Z', 1, 0): (dotmany, [('X', 1, 0), ('X', 1, 1)],
                        [('Y', 0, 0), ('Y', 1, 0)]),
 ('Z', 1, 1): (dotmany, [('X', 1, 0), ('X', 1, 1)],
                        [('Y', 0, 1), ('Y', 1, 1)])}

top 函数检查输入和输出的索引结构，并构建反映这种结构的字典，匹配键之间的索引，并创建遍历哑索引（如 j）的键列表。

就这样，我们有了一个核外点积。在这些键上调用 dask.get 会导致核外执行。

完整示例

这是一个小型的核外点积概念验证。我不期望用户编写这样的代码。我期望像 Blaze 这样的库来编写。

在磁盘上创建随机数组

import bcolz
import numpy as np
b = bcolz.carray(np.empty(shape=(0, 1000), dtype='f8'),
                 rootdir='A.bcolz', chunklen=1000)
for i in range(1000):
    b.append(np.random.rand(1000, 1000))
b.flush()

定义计算 `A.T * A`

d = {'A': b}
d.update(getem('A', blocksize=(1000, 1000), shape=b.shape))

# Add A.T into the mix
d.update(top(np.transpose, 'At', 'ij', 'A', 'ji', numblocks={'A': (1000, 1)}))

# Dot product A.T * A
d.update(top(dotmany, 'AtA', 'ik', 'At', 'ij', 'A', 'jk',
         numblocks={'A': (1000, 1), 'At': (1, 1000)}))

执行计算

>>> dask.get(d, ('AtA', 0, 0))
CPU times: user 2min 57s, sys: 6.59 s, total: 3min 4s
Wall time: 2min 49s
array([[ 334071.93541158,  250297.16968262,  250404.87729587, ...,
         250436.85274716,  250330.64262904,  250590.98832611],
       [ 250297.16968262,  333451.72293343,  249978.2751824 , ...,
         250103.20601281,  250014.96660956,  250251.0146828 ],
       [ 250404.87729587,  249978.2751824 ,  333279.76376277, ...,
         249961.44796719,  250061.8068036 ,  250125.80971858],
       ...,
       [ 250436.85274716,  250103.20601281,  249961.44796719, ...,
         333444.797894  ,  250021.78528189,  250147.12015207],
       [ 250330.64262904,  250014.96660956,  250061.8068036 , ...,
         250021.78528189,  333240.10323875,  250307.86236815],
       [ 250590.98832611,  250251.0146828 ,  250125.80971858, ...,
         250147.12015207,  250307.86236815,  333467.87105673]])

一个 7GB 的点积需要三分钟。这大约是普通内存中矩阵乘法 FLOPS 的一半。我还不确定为什么会出现这种差异。此外，这还没有使用优化的 BLAS；我们尚未利用多核。

这写起来不简单，但也还不错。

复杂性与可用性

这个系统不适合用户；它不符合 Pythonic 风格，是低级别的，而且有点 LISP 风格。然而，我相信像这样的东西将是基础设施库的合适标准。它是一个简单易用的代码目标标准。

使用像 into 和 blaze 这样的项目，我们可以为数组和表格的子问题在 dask 之上构建一个可用的高级前端。Blaze 可以生成这些字典，然后将它们交给其他系统执行。

执行

结合参考实现、多线程、HDF5/BColz 以及像 chest 这样的核外缓存系统，我认为我们可以构建一个不错的核外 ndarray 解决方案，该方案可以充分利用大型工作站的性能。

理想情况下，其他人会来构建更好的执行引擎/任务调度器。这可能是 IPython parallel 的一个合适应用。

帮助

这方面需要设计和技术反馈。什么会鼓励社区接受这样一个系统？

博客评论由 Disqus 提供支持