编写复杂的并行算法

这项工作由 Continuum Analytics 和 XDATA 项目（作为 Blaze 项目的一部分）提供支持。

tl;dr: 我们讨论如何使用复杂的 Dask 图来表达非平凡算法。我们展示了一个基于硬盘的并行 SVD 实现。

大多数并行计算都很简单

当今大多数并行工作负载都相当简单

>>> import dask.bag as db
>>> b = db.from_s3('githubarchive-data', '2015-01-01-*.json.gz')
          .map(json.loads)
          .map(lambda d: d['type'] == 'PushEvent')
          .count()

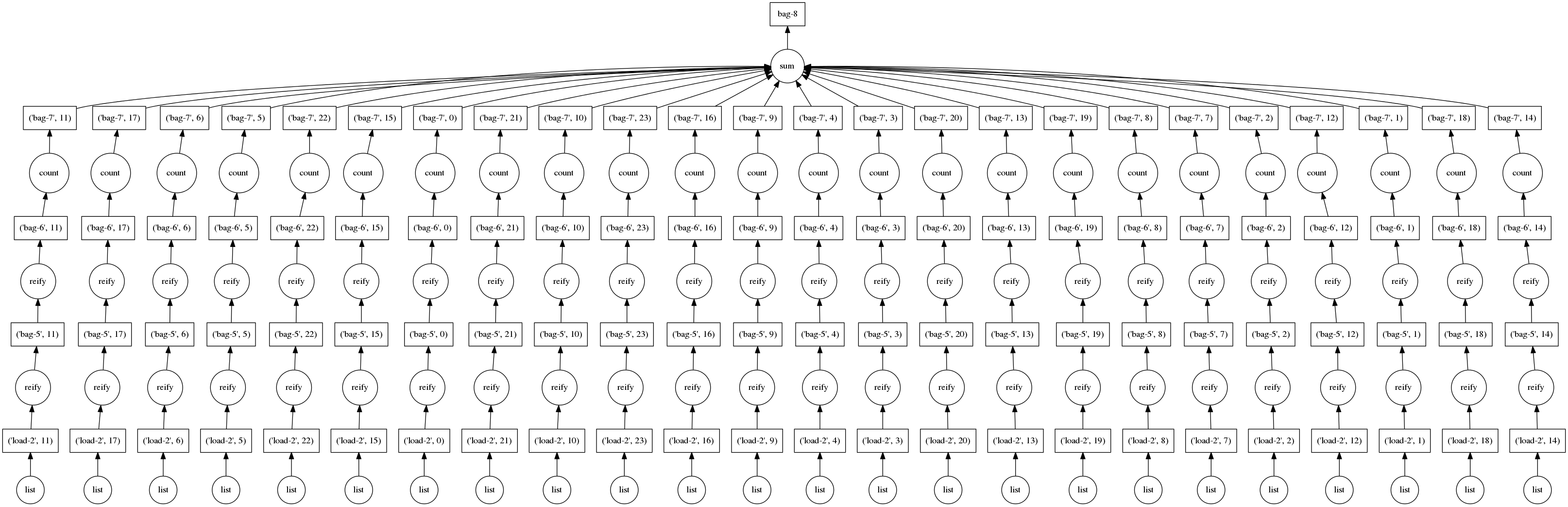
这些计算的图看起来像下面这样

这很好；这些都是可以高效并行解决的简单问题。通常这些简单的计算发生在我们的分析的开始阶段。

复杂的算法可能也很复杂

在我们分析的后期，我们需要更复杂的统计、机器学习等算法。通常这个阶段的数据可以轻松地放入内存，所以我们不必担心并行性，可以使用 statsmodels 或 scikit-learn 来处理从海量数据中提取出的千兆字节结果。

然而，如果我们的精简结果仍然很大，那么我们就需要考虑复杂的并行算法。这是一个充满令人兴奋的学术和软件工作的新领域。

示例：并行、稳定、核外 SVD

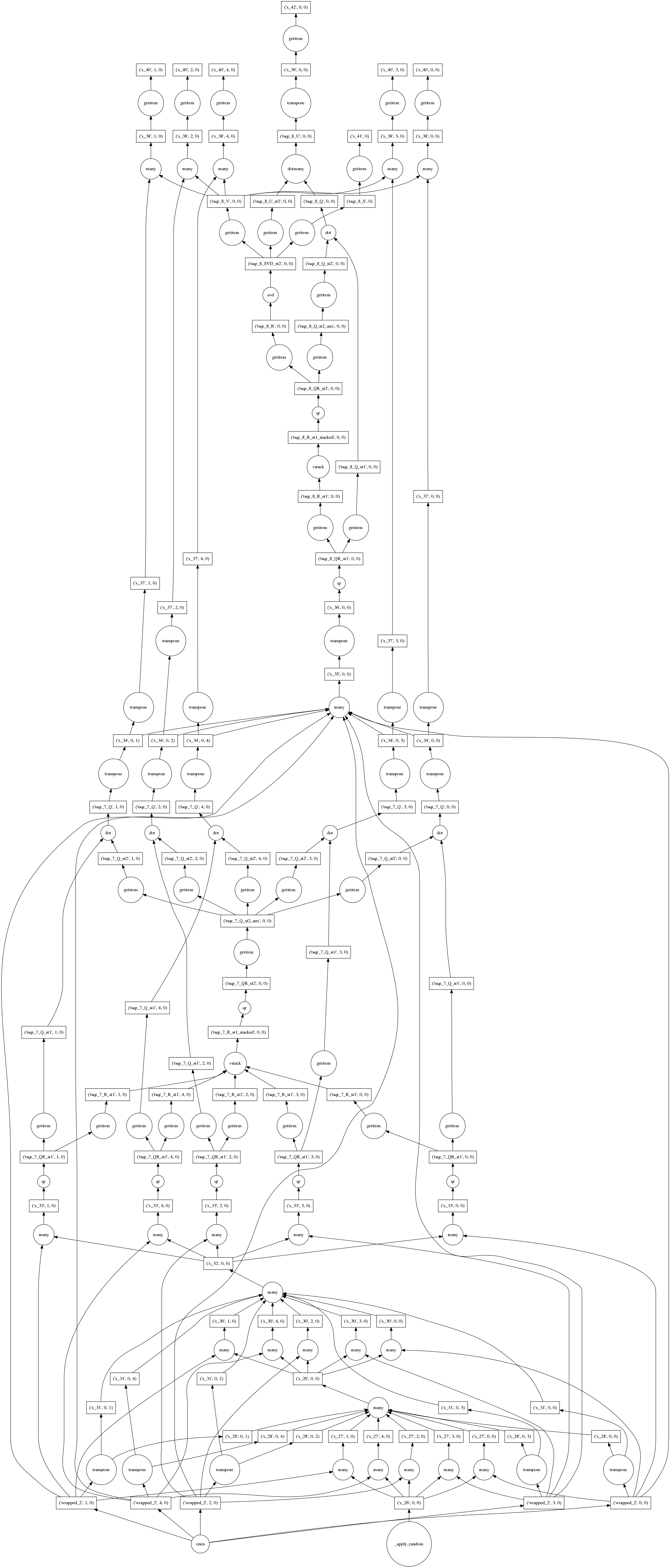
我想展示一下 Mariano Tepper 的工作，他负责 dask.array.linalg。特别地，他对奇异值分解 (SVD)（与主成分分析 (PCA) 也有很强的关联）提出了几个很棒的算法。实际上，我只是想展示这个漂亮的图。

>>> import dask.array as da
>>> x = da.ones((5000, 1000), chunks=(1000, 1000))
>>> u, s, v = da.linalg.svd(x)

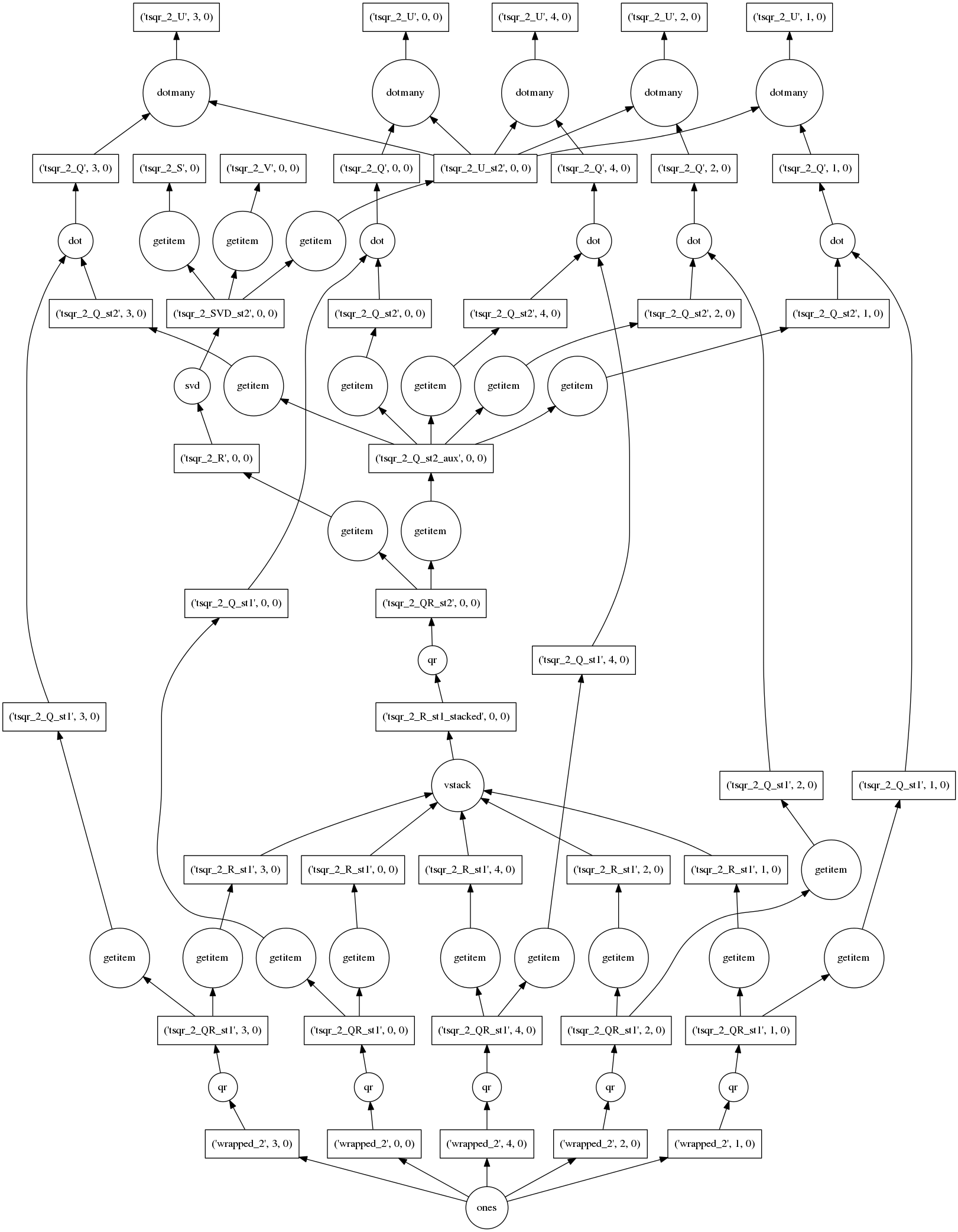
这个算法并行地以许多小块的方式计算大型高瘦矩阵的精确 SVD（精度取决于数值精度）。这使得它能够在核外（从硬盘）操作，并利用多个核心并行处理。底部我们看到构造了一个简单的全一数组，接着是对每个块的许多次 np.linalg.qr 调用。然后是大量的对各种部分的重排，包括堆叠、相乘，并进行更多的 np.linalg.qr 和 np.linalg.svd 循环。结果数组以许多块的形式在顶部和倒数第二行的位置可用。

其中一个数组 s 的 dask dict 如下所示

>>> s.dask
{('x', 0, 0): (np.ones, (1000, 1000)),
 ('x', 1, 0): (np.ones, (1000, 1000)),
 ('x', 2, 0): (np.ones, (1000, 1000)),
 ('x', 3, 0): (np.ones, (1000, 1000)),
 ('x', 4, 0): (np.ones, (1000, 1000)),
 ('tsqr_2_QR_st1', 0, 0): (np.linalg.qr, ('x', 0, 0)),
 ('tsqr_2_QR_st1', 1, 0): (np.linalg.qr, ('x', 1, 0)),
 ('tsqr_2_QR_st1', 2, 0): (np.linalg.qr, ('x', 2, 0)),
 ('tsqr_2_QR_st1', 3, 0): (np.linalg.qr, ('x', 3, 0)),
 ('tsqr_2_QR_st1', 4, 0): (np.linalg.qr, ('x', 4, 0)),
 ('tsqr_2_R', 0, 0): (operator.getitem, ('tsqr_2_QR_st2', 0, 0), 1),
 ('tsqr_2_R_st1', 0, 0): (operator.getitem,('tsqr_2_QR_st1', 0, 0), 1),
 ('tsqr_2_R_st1', 1, 0): (operator.getitem, ('tsqr_2_QR_st1', 1, 0), 1),
 ('tsqr_2_R_st1', 2, 0): (operator.getitem, ('tsqr_2_QR_st1', 2, 0), 1),
 ('tsqr_2_R_st1', 3, 0): (operator.getitem, ('tsqr_2_QR_st1', 3, 0), 1),
 ('tsqr_2_R_st1', 4, 0): (operator.getitem, ('tsqr_2_QR_st1', 4, 0), 1),
 ('tsqr_2_R_st1_stacked', 0, 0): (np.vstack,
                                   [('tsqr_2_R_st1', 0, 0),
                                    ('tsqr_2_R_st1', 1, 0),
                                    ('tsqr_2_R_st1', 2, 0),
                                    ('tsqr_2_R_st1', 3, 0),
                                    ('tsqr_2_R_st1', 4, 0)])),
 ('tsqr_2_QR_st2', 0, 0): (np.linalg.qr, ('tsqr_2_R_st1_stacked', 0, 0)),
 ('tsqr_2_SVD_st2', 0, 0): (np.linalg.svd, ('tsqr_2_R', 0, 0)),
 ('tsqr_2_S', 0): (operator.getitem, ('tsqr_2_SVD_st2', 0, 0), 1)}

所以要编写复杂的并行算法，我们只需要写下函数元组的字典。

Dask 调度器负责使用多个线程并行执行这个图。这是一个在 30000x1000 数组上进行较大计算的剖析结果

低门槛

看到这个图，你可能会想“哇，Mariano 太棒了”，他确实很棒。然而，他更是一位线性代数专家，而不是 Python 编程专家。Dask 图（只是字典）足够简单，领域专家看到它们会说“是的，我能做到”，然后写下与他领域相关的非常复杂的算法，将这些算法的执行留给 Dask 调度器。

您可以在 GitHub 上查看生成上述图的源代码。

随机化并行核外 SVD

几周前，一位基因组学研究员提出了对 SVD 的近似/随机化变体的需求。Mariano 在几天内就提供了一个解决方案。

>>> import dask.array as da
>>> x = da.ones((5000, 1000), chunks=(1000, 1000))
>>> u, s, v = da.linalg.svd_compressed(x, k=100, n_power_iter=2)

出于篇幅考虑，我将省略完整的 dict。

最后思考

Dask 图让我们能够以非常少的额外复杂性来表达并行算法。无需学习特殊的对象或框架，只需使用函数元组的字典。这使得领域专家无需被花哨的代码束缚，就能编写复杂的算法。

博客评论由 Disqus 提供支持

编写复杂的并行算法 花哨的图、数学家和 SVD

大多数并行计算都很简单

复杂的算法可能也很复杂

示例：并行、稳定、核外 SVD

低门槛

随机化并行核外 SVD

最后思考

编写复杂的并行算法花哨的图、数学家和 SVD