Dask 异步优化算法 基于部分结果演进的计算
这项工作得到了 Continuum Analytics、XDATA 项目 以及 Moore Foundation 的数据驱动发现倡议的支持。
摘要
在之前的文章中,我们使用 Dask 构建了凸优化算法,这些算法在分布式集群上高效运行,对广泛的统计和机器学习算法至关重要。
现在我们通过研究异步算法来扩展这项工作。我们将展示以下内容:
- Dask 中用于构建一般性异步计算的 API,不只是针对机器学习和优化
- 异步算法在机器学习中具有价值的原因
- 一个具体的异步算法(异步 ADMM)及其在一个玩具数据集上的性能表现
这篇博文由了解优化的 Chris White(Capital One)和了解分布式计算的 Matthew Rocklin(Continuum Analytics)合著。
异步算法 vs 阻塞算法
当我们说异步时,我们将其与同步或阻塞进行对比。
在阻塞算法中,你会发送一堆任务,然后等待结果。Dask 常规的 .compute() 接口是阻塞的。考虑以下计算,其中我们并行地对许多输入进行评分,然后找到最佳结果:
import dask
scores = [dask.delayed(score)(x) for x in L] # many lazy calls to the score function
best = dask.delayed(max)(scores)
best = best.compute() # Trigger all computation and wait until complete
这会阻塞。它运行时我们什么也做不了。如果我们在 Jupyter notebook 中,我们会看到一个小星号,表示我们需要等待。

在非阻塞或异步算法中,我们发送任务并在结果到来时跟踪它们。当计算在后台运行(或在集群中的其他计算机上运行)时,我们仍然能够在本地运行命令。Dask 有多种异步 API,但最简单的可能是 concurrent.futures API,在此 API 中,我们提交函数,然后可以等待并对它们的返回值进行操作。
from dask.distributed import Client, as_completed
client = Client('scheduler-address:8786')
# Send out several computations
futures = [client.submit(score, x) for x in L]
# Find max as results arrive
best = 0
for future in as_completed(futures):
score = future.result()
if score > best:
best = score
这两种解决方案在计算上是等效的。它们执行相同的工作并在相同的时间内运行。阻塞的 dask.delayed 解决方案写起来可能更简单,但非阻塞的 futures + as_completed 解决方案让我们更具灵活性。
例如,如果我们得到一个足够好的分数,那么我们可能会提前停止。如果我们发现某些类型的值比其他值给出更好的分数,那么我们可能会围绕这些值提交更多计算,同时取消其他计算,在执行期间更改我们的计算。
这种在执行期间监控和调整计算的能力是人们选择异步算法的原因之一。对于优化算法,我们正在进行搜索过程并频繁更新参数。如果我们能够更频繁地更新这些参数,那么我们或许能够稍微改进后续启动的每一次计算。与步进式的批量迭代算法相比,异步算法实现了集群周围信息流的增加。
异步 ADMM
在我们的上一篇博文中,我们展示了使用 dask.delayed 实现的交替方向乘子法(ADMM)的简化实现。我们看到,在分布式环境下,与更传统的分布式梯度下降相比,它表现良好。该算法的工作方式是,在我们的每个数据块上使用当前的参数估计解决一个小型优化问题,将这些结果带回本地进程,合并它们,然后根据更新后的参数发送新的计算任务。
现在我们修改此算法以异步更新,这样我们的参数会随着实时到来的部分结果而持续变化。不再是发送并等待批量结果,我们现在消耗并发出一个带有略微改进的参数估计的连续任务流。
我们依次展示三种算法:
- 同步:原始的同步算法
- 异步 - 单结果:每次有新结果到来时更新参数
- 异步 - 批量:使用自上次更新以来到来的所有结果进行更新。
设置
我们创建假数据
n, k, chunksize = 50000000, 100, 50000
beta = np.random.random(k) # random beta coefficients, no intercept
zero_idx = np.random.choice(len(beta), size=10)
beta[zero_idx] = 0 # set some parameters to 0
X = da.random.normal(0, 1, size=(n, k), chunks=(chunksize, k))
y = X.dot(beta) + da.random.normal(0, 2, size=n, chunks=(chunksize,)) # add noise
X, y = persist(X, y) # trigger computation in the background
我们定义 ADMM 的本地函数。这些对应于解决一个 L1 正则化线性回归问题
def local_f(beta, X, y, z, u, rho):
return ((y - X.dot(beta)) **2).sum() + (rho / 2) * np.dot(beta - z + u,
beta - z + u)
def local_grad(beta, X, y, z, u, rho):
return 2 * X.T.dot(X.dot(beta) - y) + rho * (beta - z + u)
def shrinkage(beta, t):
return np.maximum(0, beta - t) - np.maximum(0, -beta - t)
local_update2 = partial(local_update, f=local_f, fprime=local_grad)
lamduh = 7.2 # regularization parameter
# algorithm parameters
rho = 1.2
abstol = 1e-4
reltol = 1e-2
z = np.zeros(p) # the initial consensus estimate
# an array of the individual "dual variables" and parameter estimates,
# one for each chunk of data
u = np.array([np.zeros(p) for i in range(nchunks)])
betas = np.array([np.zeros(p) for i in range(nchunks)])
最后,由于 ADMM 不希望在分布式数组上工作,而是希望在远程 numpy 数组列表(每个 dask.array 块对应一个 numpy 数组)上工作,因此我们将每个 Dask 数组转换为一个 dask.delayed 对象列表
XD = X.to_delayed().flatten().tolist() # a list of numpy arrays, one for each chunk
yD = y.to_delayed().flatten().tolist()
同步 ADMM
在该算法中,我们发送许多任务去运行,收集它们的结果,更新参数,并重复。在这个简单的实现中,我们持续固定时间,但在实践中,我们会想要检查一些收敛标准。
start = time.time()
while time() - start < MAX_TIME:
# process each chunk in parallel, using the black-box 'local_update' function
betas = [delayed(local_update2)(xx, yy, bb, z, uu, rho)
for xx, yy, bb, uu in zip(XD, yD, betas, u)]
betas = np.array(da.compute(*betas)) # collect results back
# Update Parameters
ztilde = np.mean(betas + np.array(u), axis=0)
z = shrinkage(ztilde, lamduh / (rho * nchunks))
u += betas - z # update dual variables
# track convergence metrics
update_metrics()
异步 ADMM
在异步版本中,我们只发送足够占用所有工作节点的任务。我们随着结果的完成逐个收集它们,更新参数,然后发送一个新的任务。
# Submit enough tasks to occupy our current workers
starting_indices = np.random.choice(nchunks, size=ncores*2, replace=True)
futures = [client.submit(local_update, XD[i], yD[i], betas[i], z, u[i],
rho, f=local_f, fprime=local_grad)
for i in starting_indices]
index = dict(zip(futures, starting_indices))
# An iterator that returns results as they come in
pool = as_completed(futures, with_results=True)
start = time.time()
count = 0
while time() - start < MAX_TIME:
# Get next completed result
future, local_beta = next(pool)
i = index.pop(future)
betas[i] = local_beta
count += 1
# Update parameters (this could be made more efficient)
ztilde = np.mean(betas + np.array(u), axis=0)
if count < nchunks: # artificially inflate beta in the beginning
ztilde *= nchunks / (count + 1)
z = shrinkage(ztilde, lamduh / (rho * nchunks))
update_metrics()
# Submit new task to the cluster
i = random.randint(0, nchunks - 1)
u[i] += betas[i] - z
new_future = client.submit(local_update2, XD[i], yD[i], betas[i], z, u[i], rho)
index[new_future] = i
pool.add(new_future)
批量异步 ADMM
在有足够多分布式工作节点的情况下,我们发现客户端上的参数更新循环可能成为限制因素。性能分析后发现,我们的客户端瓶颈不是更新参数,而是计算用于下面收敛图的性能指标(因此在实践中并不是真正的限制)。然而,我们决定保留这一点,因为它对于在更大集群中可能发生的情况来说是很好的实践,在那里,更新参数的单台机器可能会被来自工作节点的大量更新淹没。为了解决这个问题,我们引入了批量处理。
我们不是逐个更新参数,而是使用到目前为止到来的所有结果进行更新。这为对抗慢速客户端提供了一种自然的防御。当客户端过载时,这种方法会平滑地将我们的算法切换回同步解决方案(尽管如此,在这个规模下我们没问题)。
方便的是,as_completed 迭代器有一个 .batches() 方法,该方法迭代到目前为止已到来的所有结果。
# ... same setup as before
pool = as_completed(new_betas, with_results=True)
batches = pool.batches() # <<<--- this is new
while time() - start < MAX_TIME:
# Get all tasks that have come in since we checked last time
batch = next(batches) # <<<--- this is new
for future, result in batch:
i = index.pop(future)
betas[i] = result
count += 1
ztilde = np.mean(betas + np.array(u), axis=0)
if count < nchunks:
ztilde *= nchunks / (count + 1)
z = shrinkage(ztilde, lamduh / (rho * nchunks))
update_metrics()
# Submit as many new tasks as we collected
for _ in batch: # <<<--- this is new
i = random.randint(0, nchunks - 1)
u[i] += betas[i] - z
new_fut = client.submit(local_update2, XD[i], yD[i], betas[i], z, u[i], rho)
index[new_fut] = i
pool.add(new_fut)
算法的视觉比较
为了展示这些算法之间的定性差异,我们包含了每个算法的性能分析图。请注意以下几点:
- 同步算法有块状的 CPU 满负荷使用,紧接着是块状的 CPU 空闲
- 异步方法更平滑
- 异步单结果更新方法在 CPU 空闲时有很多空白区域/时间。这是人为造成的,因为我们用于下方图中跟踪收敛诊断的代码效率低下,并且位于客户端内循环中
- 我们故意保留了这段低效的代码,这样我们就可以在第三个图中通过批量处理来减少这种浪费,第三个图更加饱和。
您可以使用每个图右上角的工具进行放大。您可以通过点击“View full page”链接在完整窗口中查看完整性能分析。
同步
异步 - 单结果
异步 - 批量
绘制收敛标准
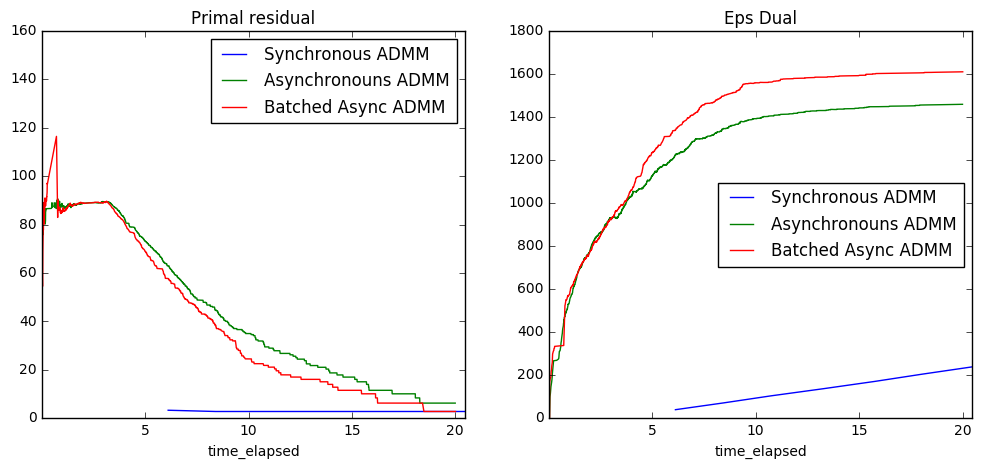
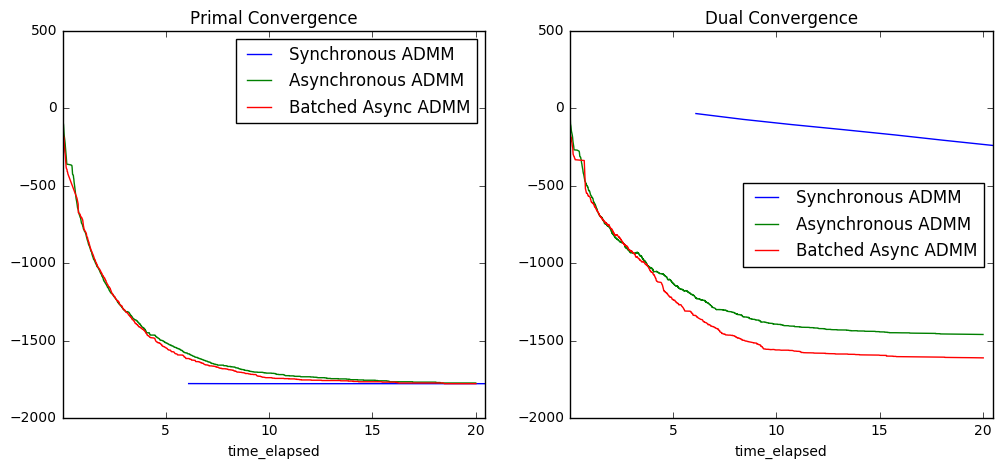
分析
为了更好地理解这些图传达的信息,回忆一下,优化问题总是成对出现的:原始问题通常是主要关注的问题,而对偶问题是一个密切相关的问题,它提供了关于原始问题中约束条件的信息。也许最著名的对偶例子是图论中的最大流最小割定理。在许多情况下,同时解决这两个问题可以带来性能提升,这正是 ADMM 试图做到的。
在我们的例子中,原始问题中的约束条件是:所有工作节点必须就最优参数估计达成一致。因此,我们可以将对偶变量(每个数据块一个)视为衡量各自数据块达成一致的“成本”。直观地说,它们会从小开始并逐步增长,以找到每个工作节点达成共识的正确“成本”。最终,它们会在最优成本处趋于平稳。
那么
- 原始残差图衡量不一致的程度;“小”值意味着一致
- 对偶残差图衡量达成一致的总“成本”;这会增加,直到找到正确的成本
这些图告诉我们以下几点:
- 异步算法达成一致的成本更高,这是合理的,因为每个工作节点总是使用稍微过时的全局参数估计进行工作,这使得达成共识更加困难
- 阻塞 ADMM 在 5 秒刚过之后才开始更新,而异步算法已经有时间收敛了。(在处理实际数据时,我们可能会指定所有工作节点每 K 次更新后需要报告一次。)
- 异步算法需要一些时间让信息充分扩散,但一旦信息扩散完成,它们会迅速收敛。
- 异步和同步算法几乎立即收敛;这很可能是因为数据具有高度同质性(这些数据是为了很好地拟合模型而生成的)。我们的下一个实验应该使用真实世界的数据。
我们可以做得更好的地方
从分析角度看,通过在不像当前玩具数据集那样同质的真实世界数据集上执行相同的实验,我们期望得到更丰富的结果。
从性能角度看,通过做两件事,我们可以获得更好的 CPU 饱和度:
- 不运行我们的收敛诊断代码,或者让它们快得多
- 当我们只更新了少量元素时,不计算完整的
np.mean遍历所有 beta。相反,我们应该维护这些结果的运行聚合。
进行了这两个改变(每个都很容易)后,我们相当有信心可以扩展到相当大的集群,同时仍然能使硬件饱和。
博客评论由 Disqus 提供支持